
Interview
The Shape of Donuts, the Universe, and Everything
In his book Math Without Numbers, an accessible introduction to abstract mathematics, author Milo Beckman takes the sting out of learning math
How you feel about math likely comes down to what you feel about numbers, because math is all about numbers, right? One plus one equals two. 21 divided by 3 equals 7. Fractions. Percentages. It's all numbers!
But what if you could learn math without numbers? It sounds insane, but there's a whole world of math that not only goes beyond the algebra—or applied math—we all learned in school; in fact, it's barely interested in it. Abstract mathematicians deal with concepts like manifolds (a shape with no special points, such as a beginning or end), the continuum (unthinkably bigger than infinity), and automata (worlds made of math). It's work more rooted in theory and philosophy than cold, hard numeracy: who cares about fractions if fractions are just man-made constructs and not pure math? At its core, this kind of math is still problem-solving, only instead of working out the square footage of your living room, what's at stake is the shape and scope of the world around us, from the donuts we have for breakfast (which are torus manifolds, by the way) to the dimensions of the universe. And numbers hardly ever factor into the equation.
It's all wild, expansive, and, at times, mind-bending, and it's easy to be scared off by it. But Milo Beckman's new book, Math Without Numbers, released earlier this month, is the ideal atlas for this frontier.
And the 25-year-old author is the ideal guide. Beckman began taking math classes at New York's elite Stuyvesant High School when he was 8; was captain of the New York City Math Team at 13; completed Harvard's graduate-level math sequence when he was 16; and after working at three tech companies and two banks, retired, at 19, to teach math in New York, China, and Brazil. Beckman's experience with and enthusiasm for abstract math is present on every page of his book, and his youth and perspective blow up the stuffy-academic stereotype and allow him to craft a welcoming and encouraging space to encounter these bizarre and challenging topics. It also helps that the 200-page book is stuffed with drawings by M Erazo, to help make sense of all this.
Beckman spoke with The Elective about Math Without Numbers, how math can help order your everyday life, the state of American math education, and why some mathematicians have beef with fractions.

Portia Lundie (Beckman), Penguin Random House (cover)
Why did you write this kind of book about math?
I really wanted to reclaim the word "math." Most people hear "math" and they're thinking of school math: arithmetic, multiplication tables, computations; trying to do what a computer can do. And that's really not what mathematicians are interested in. It's not what we care about. It's not what we like to think about. I think people have this idea that mathematicians spend their days doing really long division problems on paper, so the first thing I wanted to do is say, Okay, here's this other kind of math that you may not have had access to.
I feel very lucky to have had access to this extracurricular world of math throughout my life. It's about collaborative problem-solving, it's about inventing this wacky new world where you can sort of set the rules and the guidelines and then explore it. At its core, it's really fun and creative and it’s really not captured in the math curriculum in schools or in the way our culture talks about math, and that was a long-standing frustration for me as someone who just did a lot of math. I wanted to give people who might not necessarily want to be mathematicians something like a museum tour, where you get to walk around and see, "Oh, that's kind of cool," and then, if you're inspired to do some math, there are plenty of other books you can pick up afterwards. But you also have the option to read this, look at some pretty pictures, get some cool ideas, and walk away with just a new understanding of what math is and how it fits into the rest of the world.
How did you write this book? The kind of math you're talking about is pretty conceptual.
The process was pretty roundabout. I’ve wanted to write a sort of wacky, fun book about math since I was very, very young, something like 8 or 10. I put it on hold because my education taught me that that wasn't so serious of a thing to do. After graduating, I was teaching math through a couple of different venues and had the opportunity to develop my own curriculum and teach whatever kind of math I wanted to teach, and it all just came back to the same idea. So what I ended up doing is—and this was my friend's idea—I went to an art store and bought, like, a 20-foot scroll and just started drawing pictures. So the first draft of this book was math without numbers, and also without words. I filled up this scroll with a bunch of pictures of different math shapes and concepts and structures that I liked talking about and teaching and, I thought, "Oh, this looks like a book.”
How did you settle into this form as opposed to, say, a graphic novel?
Well, it sort of is a graphic novel. I mean, it's not a graphic novel, but there's an illustration on almost every page. I think it came out to like 173 illustrations, and the book is only 200 pages long. There are a lot of ways to read the book. You don't have to read it from start to finish. You can read a chapter standalone or you can just flip through and look at the pictures and find a picture you like and say, "Huh, I wonder what that's about." There are also all these little puzzles and bonus materials and little games. I definitely wanted it to be an easy read that you can pick up and put down and finish in a few sittings, but also something that has a real visual feel to it. For the interior design, I worked with the illustrator M Erazo, who's a really fantastic artist. Once the manuscript was edited, the two of us sat down over Zoom—this was in April—and went into InDesign and designed every page ourselves. That was a really fun process, to have that kind of visual control over the finished product.
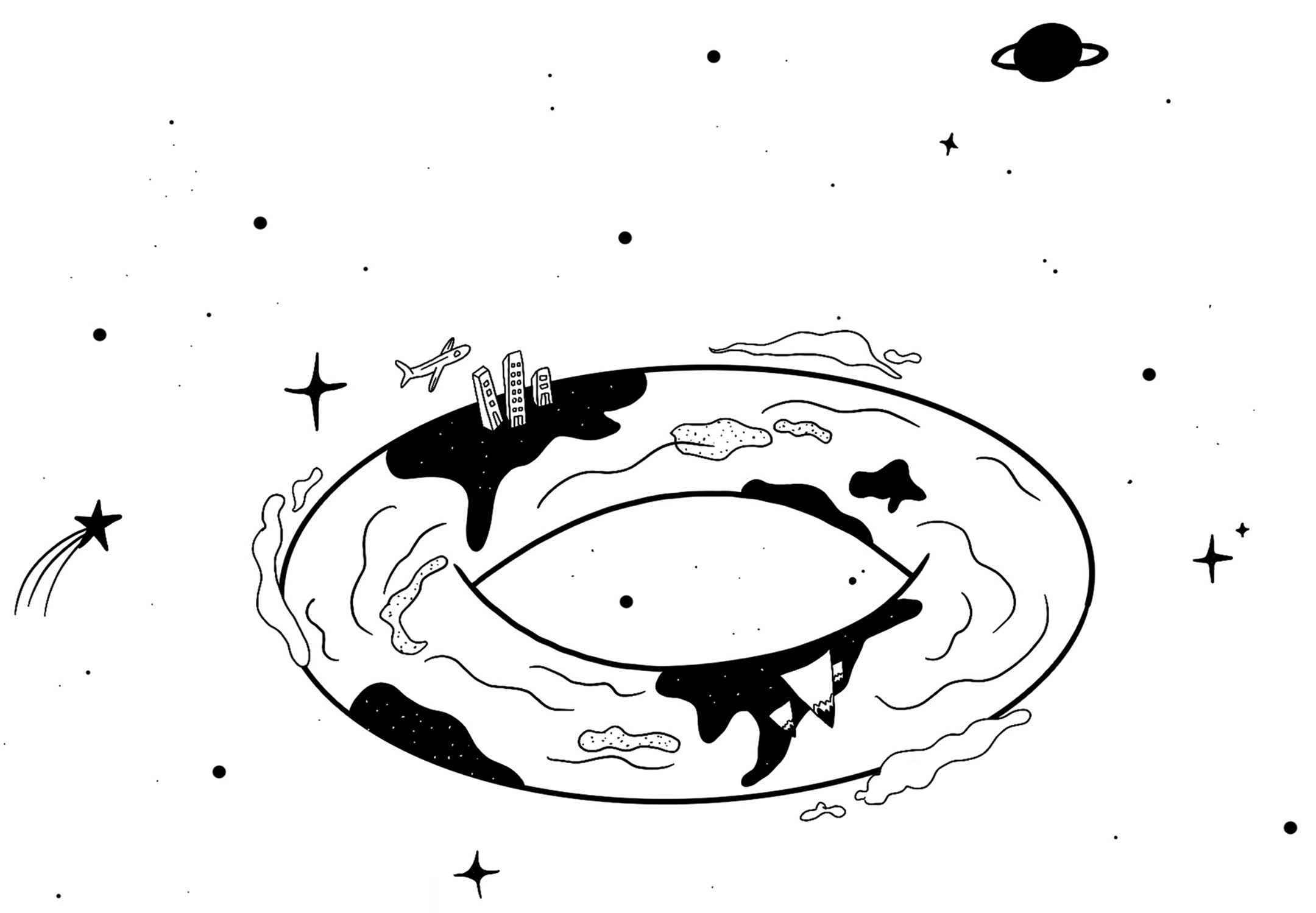
Illustration by M Erazo
An illustration from "Math Without Numbers" depicting Earth as a torus manifold.
How did you and M find each other?
Publishers have in-house illustrators who are fantastic, but I knew I didn't want the book to have textbook-like math diagrams with clean lines and everything. I wanted it to be a little bit more notebook-scratchy or blackboardy, so I was clear from early on that I wanted to find an illustrator myself. M was the second person I met with, and I was blown away by their level of professionalism and aesthetic. They have a fantastic Instagram account and they make some really cool, trippy, colorful, spacey visuals. That really tracked with me and how I think about math and the way that I feel a lot of people in this math world think about this kind of mathematical universe. It's this kind of, like, fictional, otherworldly landscapes with weird manifolds and dimensions and stuff. I really liked what I was seeing from M in the first few sample illustrations, and it ended up being a really fun collaboration. I basically drew all of these in a notebook-doodle kind of way and scanned them and sent them over to M, and then we'd go back and forth on them. The illustrations took about as much time and effort as the words, but that was really fun.
The book started as a scroll of illustrations, but why was it important to keep the illustrations as part of this book?
Math is a very visual subject and I think it's often not taught that way, especially when you get to college-level, graduate-level math, you always get really confused, or at least I got super-confused, because they'll give you these definitions that are stated very precisely in almost legalese-sounding terms, and you can say, "OK, so a manifold is a topological space, which is locally Euclidean," and then you're like, "OK, what does that mean? What's ‘locally Euclidean?’" You have to look back a couple pages to see what this means, and then you're, like, "OK, Euclidean is defined in terms of this other term," and you have to keep looking around. You finally piece it together after an hour, and you're like, "Well, why don't you just draw me a picture?" So what I wanted to do here is just draw the picture. A lot of these concepts are kind of bizarre and novel ideas that you don't really encounter in your daily life, so having the visual component is a very easy way to drop into this world without having to dive into all the nitty gritty details of the math behind it.
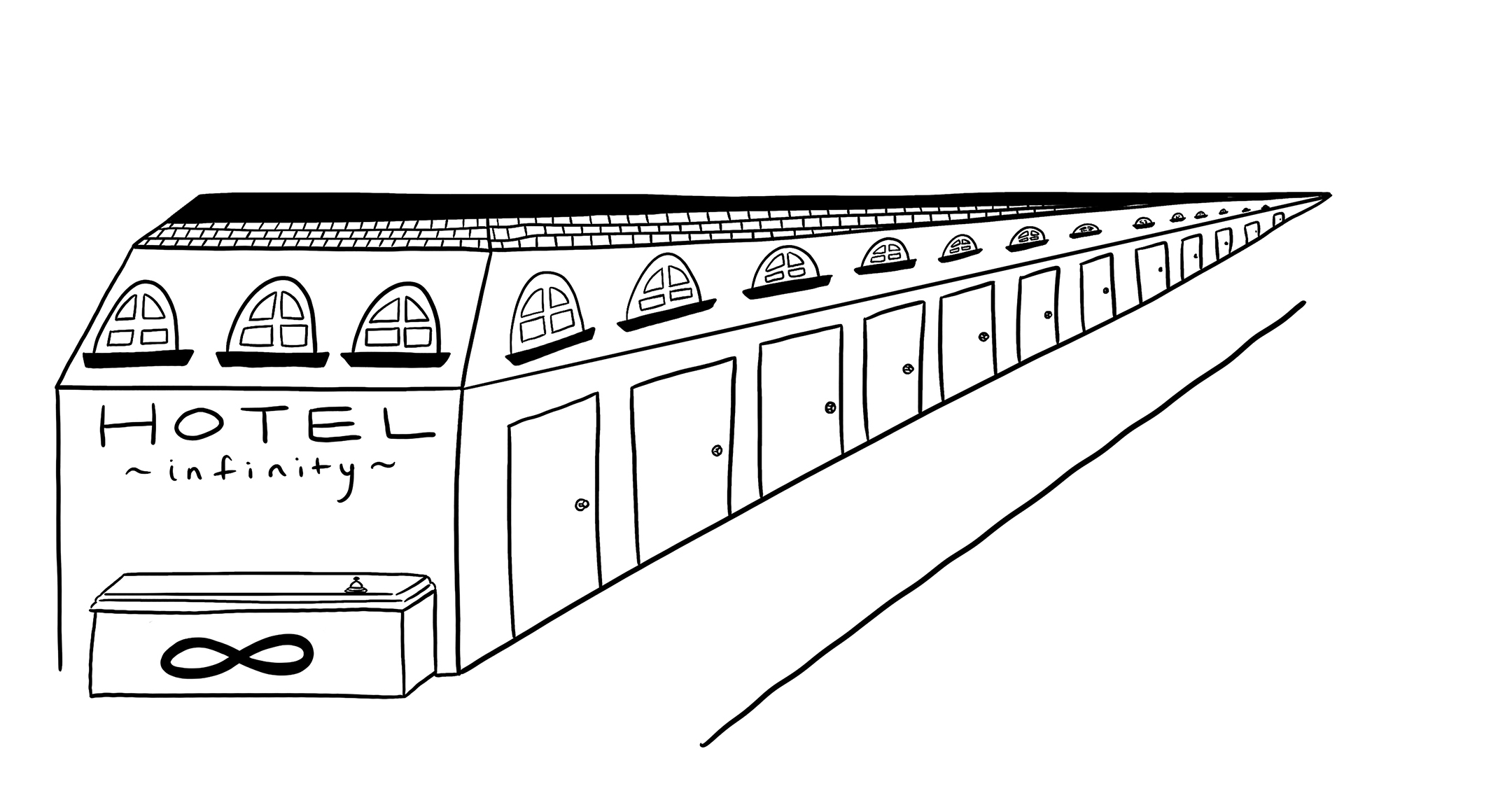
Illustration by M Erazo
An illustration from "Math Without Numbers" to help explain the concept of the continuum.
And true to the title, this is a book about math with no numbers.
Math is not really about numbers. I think that's a secret you don't get to know unless you go to what people call higher math, which I think is a kind of pretentious term. It really just means abstract math. I never really took too strongly to the numbers side of math; that was always my least favorite part of it. I had this issue when I was on math team, where you're working on a problem, the whole team is counting on you, and I would come up with some clever idea, I would solve the problem, and then in the end would do, like, three times three equals three or something ridiculous like that, and I would get the whole problem wrong. Arithmetic was not my strong suit. People would say, "What do you mean, you're good at math but you're not good with numbers? How can that be?" So I wanted to give a sense of what math without numbers looks like.
Numbers are what we really focus on, especially in the grade-school educational program. It's about numeracy, and I think that's important for getting around in your daily life. You need to know how taxes work, how credit works, you need to know the basics of numbers that we interact with on a day-to-day basis. I would say that that's also not really taught in school. But this other side of math, this theoretical math that's about the infinite, symmetries, logic, structures, order, that kind of stuff is definitely skimmed over and it's kind of implied that it's reserved for brainiacs and people who put all this work in and go through a hazing process in order to get access to this cool stuff. I don't think that's necessary. I think you can really easily get a glimpse into what these topics are about without having to go through the wringer.
It's clear why we need to know how to handle everyday situations where numbers are important. But what's the value to our everyday lives of knowing about, say, manifolds or the continuum?
Right, what's the point? That's the biggest question. The first answer is kind of a letdown, and it's that for most mathematicians, there is no point. For most mathematicians, the point is just the math itself. They would say, “Well, you wouldn't ask a poet, what's the point of poetry?” They see math as this beautiful thing that's worth exploring on its own merits. I think that answer has some value, but I don't think that's particularly useful to people who don't have that perspective. So the answer that I will give on why it's been helpful for me, is... I stopped doing math academically about eight years ago. Once I completed the graduate course sequence, they wouldn't let me transfer my credits, so I majored in government. What I found is that math and the experience of this extracurricular math world of math team and math camp, which is founded on this concept, again, of collaborative problem-solving, gave me a way of approaching problems in general. It gave me a way of organized thinking, of thinking in slow motion, of taking a situation, breaking it down into its core important components, simplifying it, sanding away all the rough edges, and just sort of logicking it out from that perspective. I've found that lens incredibly useful across a number of fields of academic inquiry, but also just in my day-to-day life. You can approach so many issues in your daily life from the perspective of a mathematician. You don't necessarily have to be doing math in order for those tools and strategies to be useful.
You've experienced math as a student, tutor, and now author. What do you see as the strengths and weaknesses of math education in the United States?
I think—and I would say that most mathematicians and math educators would agree with me—that the current state of math education in the United States is abysmal. I don't blame it on the teacher; I don't even blame it on any person in particular. I just think we're caught in this weird infinite loop, reteaching the same curriculum that was set in stone around 1920, which was in turn based on this English grammar school math education, which in turn was based on this idea of what it meant to be a European scholar. Everyone has to learn Euclidean geometry and everyone has to learn these particular tools that maybe were useful back before we had slide rules and then calculators. But now, for the most part, the stuff that you're learning in school is just how to be a less-efficient calculator. And that really bums me out. The other thing that's really upsetting is that it’s presented as a hurdle you have to jump over to graduate and achieve your dreams and live the life you want. For that reason, I think, people find math scary and daunting. And also the way it's presented as a competition, you're graded from zero to 100 and you're ranked and people associate your math scores with intelligence, which I think is pretty wack, too.
There's a lot that we do to make math really unappealing and terrifying to people. That's not universal. I taught math in China and was shocked to see the completely different attitude people have there, where the students were embarrassed to not know math. If you didn't know math, that's sort of a social problem where people were, like, "What, you couldn't figure out the math homework? What's wrong?" It's almost the opposite of what I see in the United States. I've often had students, especially female students—it's a very gendered issue—who will say, "Oh, math isn't for me," or, "Oh, I don't have the mind for math," or, "I just don't like doing math." I think it's really harmful. There are a lot of tropes surrounding that, where we have this idea of the math prodigy and we should just leave it to them. It's a bummer. Math is universal, and everyone should have access to it without it being this terrifying monster.

FPG/Getty Images
Students at the Henry Ford Trade School in Dearborn, Michigan being taught shop trigonometry in the 1940's.
How would you reshape math education?
It's a question that I can answer, but my answer is so out there that it's almost useless. I would say most of early elementary and middle education should be focused on creative problem-solving—logic puzzles, doing origami; there are all kinds of ways to teach math and the sort of mental structures, the way of thinking that math is meant to teach, without it being about drilling. It's good to have a little bit of mental arithmetic skills to get by. And once you get to high school, everyone should be able to do these basic survival math classes. I think everyone needs to learn accounting, taxes, credit. And the kind of stuff that's in this book should be available to everyone—but people shouldn’t be forced to take it. I think it should be an elective and people should be excited about it and want to take it.
I don’t think you should teach people things they don't want to know—I don't think you can teach people things they don't want to know. I think the best role of the teacher is to provide the resources for a student to achieve the full extent of their curiosity. The sort of factory farm process we have of giving teachers this instruction of just make these students know math, I don't think that happens. I think a student has to come to you wanting to know math, and then you give them the opportunity. The early math curriculum should be focused on building that excitement and curiosity with games and puzzles, and then later on people should be given survival skills and the opportunity to be recreational.
Math can be applied everywhere and it already shows up in other classes, especially sciences like chemistry and physics. But do you think math would benefit from being introduced in other, more liberal arts courses like history or English?
It's an interesting question. I think there's a tendency for math and STEM subjects to want to invade other fields. I think there are cases where you could benefit from that, but I'm not totally sure history class is in need of more math. But I think education in general should be less divided into subjects. At the end of the day, what you're studying is existence, reality, and there are many ways to approach that. History can't be separated from psychology can't be separated from biology can't be separated from literature can't be separated from music. There’s interplay between all of these things, so I'm all in favor of more interaction between the subjects and the fields, both at the grade school and the university level.
In one chapter, you write there are people who think fractions are suspicious. Can you explain that, because it sounds bananas?
There's a famous quote—I forget who said this, I'm sure it's someone important—that God gave us the natural numbers and everything else is a human invention. Meaning basically, yeah, there's 1, 2, 3, 4, 5, et cetera, but once you go past that you're just making stuff up. You can have three apples, and that's a real thing. But two-thirds of something is inherently an approximation. Or something like that—I haven't read deeply into this argument. But people really make these pretty bizarre claims—or, from my perspective they're bizarre; from their perspective they're perfectly reasonable.
One of my favorites is this concept of extreme finitism. Finitism is a pretty popular philosophy, the idea that we should not be dealing with infinities. A lot of calculus analysis, set theory deals with the concept of infinity, and mathematicians have gotten very comfortable with talking about infinity, but there are some mathematicians, some who are very famous, and some philosophers who say, "Don't do that. You can't work with infinity in that way. You're going to eventually hurt yourself." And there's this other branch of that, which I think only a couple of people have really hitched their ride to, which I think is called strong finitism, which is basically not just that infinite quantities don't exist but very, very, very large numbers don't exist. You might say that once you go past, say, the number of particles in the universe, everything past that is purely imaginary. When we talk about numbers as going on forever, as every integer has a next integer, that might only be true in a limited sense. And I always found that fascinating, just as an example of how much is uncertain—how even in math, in order to make claims, you need to start with some base assumptions. You can't just pull the rabbit out of thin air.
This conversation has been edited for length and clarity.


